图4－4－4

三颗人造地球卫星A、B、C在同一平面内沿不同的轨道绕地球做匀速圆周运动，且绕行方向相同，已知R_A＜R_B＜R_C.若在某一时刻，它们正好运行到同一条直线上，如图4－4－4所示．那么再经过卫星A的四分之一周期时，卫星A、B、C的位置可能是(　　)

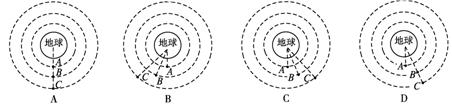
答案：C

2．(2009·全国Ⅰ，19)天文学家新发现了太阳系外的一颗行星．这颗行星的体积是地球的4.7倍，质量是地球的25倍．已知某一近地卫星绕地球运动的周期约为1.4小时，引力常量G＝6.67×10^－11 N·m²/kg²，由此估算该行星的平均密度约为(　　)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A．1.8×10³ kg/m³     B．5.6×10³ kg/m³     C．1.1×10⁴ kg/m³   D．2.9×10⁴ kg/m³

解析：近地卫星绕地球做圆周运动时，所受万有引力充当其做圆周运动的向心力，即：G＝m²R，由密度、质量和体积关系M＝ρ·πR³解两式得：ρ＝≈5.60×10³ kg/m³.由已知条件可知该行星密度是地球密度的25/4.7倍，即ρ＝5.60×10³× kg/m³＝2.9×10⁴ kg/m³.

答案：D

3．质量相等的甲、乙两颗卫星分别贴近某星球表面和地球表面围绕其做匀速圆周运动，已知该星球和地球的密度相同，半径分别为R和r，则(　　)

A．甲、乙两颗卫星的加速度之比等于R∶r 

B．甲、乙两颗卫星所受的向心力之比等于1∶1

C．甲、乙两颗卫星的线速度之比等于1∶1 

D．甲、乙两颗卫星的周期之比等于R∶r

解析：由F＝G和M＝ρπR³可得万有引力F＝GπRmρ，又由牛顿第二定律F＝ma可得，A正确．卫星绕星球表面做匀速圆周运动时，万有引力等于向心力，因此B错误．由F＝GπRmρ，F＝m可得，选项C错误．由F＝GπRmρ，F＝mR可知，周期之比为1∶1，故D错误．

答案：A

4.