一、单项选择题(本题共4个小题，每小题4分，共16分．每小题给出的四个选项中，

只有一个选项符合题目要求)

1．(2010·浙江五校联考)如图1所示，三个固定的斜面底边长度都相等，斜面倾角分别

为30°、45°、60°，斜面的表面情况都一样．完全相同的物体(可视为质点)A、B、C

分别从三斜面的顶部滑到底部，在此过程中                                            (　　)

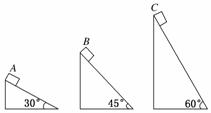
图1

A．物体A克服摩擦力做的功最多

B．物体B克服摩擦力做的功最多

C．物体C克服摩擦力做的功最多

D．三物体克服摩擦力做的功一样多

解析：设斜面底边长度为b，则W_f＝－μmgcosθ·＝－μmgb，即克服摩擦力做功

为定值W_f′＝μmgb，只有D正确．

答案：D

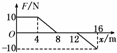2．(2010·黄冈预测)质量为10 kg的物体，在变力F作用下沿x

轴做直线运动，力随位移x的变化情况如图2所示．物体在x

＝0处速度为1 m/s，一切摩擦不计，则物体运动到x＝16 m处

时，速度大小为                                                             (　　)       图2

A．2 m/s　　　　　　          B．3 m/s

C．4 m/s                                            D. m/s

解析：力－位移图象下的面积表示功，由图象可知，一部分正功与另一部分负功抵消，

外力做的总功W＝Fx＝40 J，根据动能定理W＝mv²－mv₀²，得v＝3 m/s.B项正确．

答案：B

3．(2010·三水中学月考)一个质量为m的物体，从倾角为θ、高为h的斜面上端A点，

由静止开始下滑，到底端B点时的速度为v，然后又在水平面上滑行s位移后停止在

C点，物体从A点开始下滑到B点的过程中克服摩擦力所做的功及物体与水平面间的

动摩擦因数分别为                                                                                      (　　)

A．mg－，　　　　　　 B．mgh－，

C．mgh＋，                    D．mgh＋，

解析：设由A到B过程，物体克服阻力做功为W_f，由动能定理得：mgh－W_f＝mv²

－0，得出W_f＝mgh－mv²，由B到C的过程中，由动能定理得：－μmgs＝0－mv²，

解得：μ＝，故只有A正确．

答案：A

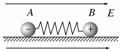4．如图3所示，质量相等的两个小球A、B，带有等量异种电荷，

通过绝缘轻弹簧相连接，整个装置放在绝缘光滑的水平面上，

当突然加一水平向右的匀强电场后，两小球A、B将由静止          图3

开始运动，在以后的整个运动过程中，对两个小球和弹簧组成的系统(设在以后的整个

运动过程中弹簧形变都不超过弹性限度)，以下说法正确的是                          (　　)

A．系统动量不守恒，机械能一定不断减小

B．系统动量守恒，机械能一定不断增加

C．当弹簧长度达到最大值时，系统机械能一定最小

D．系统动能最大时，A小球所受的合电场力与弹簧对A的弹力一定大小相等

解析：两小球所受合外力为零，动量守恒，且机械能先增大后减小(电场力先做正功后

做负功，弹簧伸长最大时机械能最大)．从开始运动到电场力等于弹簧弹力时，合力一

直做正功，小球动能一直增大．D正确．

答案：D