|
一、 内容黄金组
1． 知道曲线运动中速度的方向，理解曲线运动是一种变速运动．
2． 知道物体做曲线运动的条件是所受合外力的方向与它的速度方向不在一条直线上．
3． 知道什么是合运动，什么是分运动．知道合运动和分运动是同时发生的，并且不互相影响.
4． 知道什么是运动的合成，什么是运动的分解.理解运动的合成和分解遵循平行四边形定则．
5． 会用作图法和直角三角形知识解有关位移和速度的合成、分解问题．
二、 要点大揭秘
1． 曲线运动
轨迹是曲线的运动叫曲线运动，对曲线运动的了解，先应知道三个基本点：
（1） 曲线运动的速度方向时刻在改变，它是一个变速运动。
（2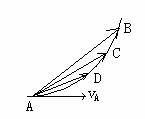）  做曲线运动的质点在轨迹上某一点（或某一时刻）的瞬时速度的方向，就在曲线这一点切线方向上。
对此除可通过实验观察外，还可用到在瞬时速度中讲到的“无限分割逐渐逼近”的思想方法。如图所示，运动质点做曲线运动在时间t内从A到B，这段时间内平均速度的方向就是割线AB的方向，如果t取得越小，平均速度的方向便依次变为割线AC、AD。。。。的方向逐渐逼近A处切线方向，当t= 0时，这极短时间内的平均速度即为A点的瞬时速度vA，它的方向在过A点的切线方向上。
（3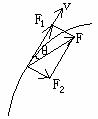）  做曲线运动有一定条件，这就是运动物体所受合外力 F与它的速度v夹成一定的角度，如图所示，只有这样，才可能出现垂直于速度v的合外力的一个分力，这个分力不能改变v的大小，但它改变v的方向，从而使物体做曲线运动。
2． 运动的合成和分解
（1） 运动的合成首先是一个实际问题，例如轮船渡河的运动就是由两个运动组合成的，另外，运动的合成和分解是一种研究复杂运动的基本方法――将复杂运动分解为两个方向上的直线运动，而这两个直线运动的规律又是我们所熟悉的，从而我们通过运动合成求得复杂运动的情况。
（2） 运动合成的目的是掌握运动，即了解运动各有关物理量的细节，所以运动的合成在实际问题中体现为位移、速度、加速度等基本物理量的合成。由于这三个基本量都是矢量，它们的运算服从矢量运算法则，故在一般情况下，运动的合成和分解都服从平行四边形定则，当分运动都在同一直线上时，在选定一个正方向后，矢量运算可简化为代数运算。
（3） 运动的合成要注意同一性和同时性。只有同一个物体的两个分运动才能合成。此时，以两个分运动作邻边画出的平行四边形，夹在其中的对角线表示真实意义上的合运动，不同物体的运动由平行四边形定则得到的“合运动”没有物理意义。只有同时进行的两个运动才能合成，分运动和合运动同时发生，同时结束。 |
