固体  液体  气体

能力素质

【例1】两端封闭内径均匀的直管长为L，管中有一段长为h的水银柱将管隔成两部分，已知L＝4h，如图13－89所示，在温度为27℃时，管A上B下竖直的放置，B端气柱长LB＝h，若温度不变，B不动，A转过60°角时，B端气柱长L′B＝2h．问：当管A上B下竖直放置，温度77℃时，B端气柱长L′B＝？(用h表示)

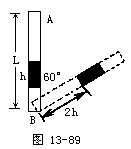
解析：以A端和B端气体为研究对象，根据题意和玻意耳定律：

pA·2h＝pA′·h即pA′＝2pA

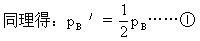
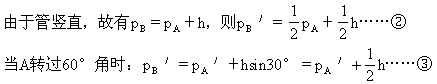
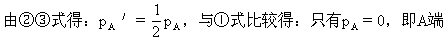
管内为真空．

由此得B端气体在27℃和77℃时压强均为h cmHg，根据盖·吕萨

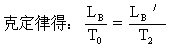
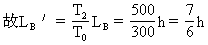
点拨：解答此题时分析出A端为真空是关键，对于这样的问题，从探索题中应满足的条件入手是解题的重要途径．

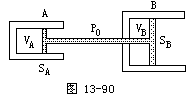
【例2】如图13－90所示，在固定的气缸A和B中分别用活塞封闭有一定质量的理想气体，活塞面积之比SA∶SB＝1∶2，两活塞以穿过B的底部和刚性细杆相连，可沿水平方向无摩擦滑动，两个气缸都不漏气．初始时A、B中气体的体积皆为V0，温度皆为T0＝300K，A中气体压强pA＝1.5p0，p0是气缸外的大气压强，现对A加热，使其中气体的压强升高pA′＝2.0P0，同时保持B中气体的温度不变，求此时A中气体温度TA′．

解析：对活塞分析有：

pASA＋pBSB＝p0(SA＋SB)  ①

pA′SA＋pB′SB＝p0(SA＋SB)  ②

对B中气体因发生等温变化，有pB′·VB＝pBV0  ③

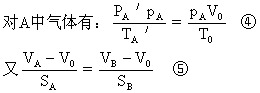
联立以上各式，代入数据解得：TA′＝500K

点拨：气缸中用活塞封闭气体时，通常由活塞受力情况求气体压强，对两部分相关联的气体分别使用状态方程，再全力找出两部分气体的联系，这就是求解气体连结体问题的基本思路．