|
赣马高级中学2011届高三考点突破专题十八常见的数学思想方法
常见的数学思想方法(3)
040整体法、特殊化
[自我提醒]
解数学题时,人们往往习惯于从问题的局部出发,将问题分解成若干个简单的子问题,然后再各个击破、分而治之.但思考方法并非对所有题目都适用,它常常导致某些题解题过程繁杂、运算量大,甚至半途而废.其实,有很多数学问题,如果我们有意识地放大考察问题的“视角”,往往能发现问题中隐含的某个“整体”,利用这个“整体”对问题实施调节与转化,常常能使问题快速获解.一般地,我们把这种从整体观点出发,通过研究问题的整体形式、整体结构、整体特征,从而对问题进行整体处理的解题思想方法,称为整体思想方法.
辩证唯物主义认识论认为,从特殊到一般,从具体到抽象,这是人们普遍遵循的认识规律,对一般或抽象复杂的数学问题,采用“以退为进”的策略,通过特殊的情形、简单的事例探求问题的结论,这一思想称为数学解题中的特殊化思想
[自我检测]
1.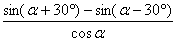 的值为___ _____. 的值为___ _____.
2.已知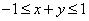 , ,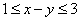 ,则 ,则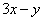 的取值范围是___ _____. 的取值范围是___ _____.
3.过△ABC的重心任作一直线分别交AB、AC于点D、E,若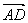 =x =x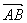 , ,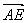 =y =y ,xy≠0,则+的值为___ _____. ,xy≠0,则+的值为___ _____.
4.四面体的六条棱中,有五条棱长都等于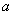 ,则该四面体的体积的最大值___ _____. ,则该四面体的体积的最大值___ _____.
5.已知数列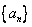 对于任意 对于任意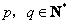 ,有 ,有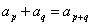 ,若 ,若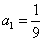 ,则 ,则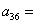 ___ _____. ___ _____. |

