|
23.圆中成比例的线段
知识考点:
1、相交弦定理、切割线定理、割线定理是圆中成比例线段的重要的结论,是解决有关圆中比例线段问题的有力工具。
2、掌握和圆有关的比例线段的综合运用,主要是用于计算线段的长。
精典例题:
【例1】已知如图,AD为⊙O的直径,AB为⊙O的切线,割线BMN交AD的延长线于C,且BM=MN=NC,若AB=2。求:
(1)BC的长;
(2)⊙O的半径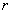 。 。
分析:由题设图形不难可以看出在本题中可综合运用勾股定理、切割线定理、割线定理来解题。

解:(1)设BM=MN=NC=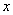 ,由切割线定理可得: ,由切割线定理可得: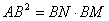
即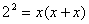 解得: 解得: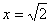 ,∴BC= ,∴BC=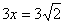 ; ;
(2)在Rt△ABC中,AC=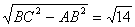
由割线定理可得: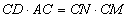
∴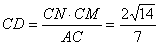
∴
【例2】如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠BAC的平分线与BC和⊙O分别交于点D和E,求 的值。 的值。
分析:由切割线定理有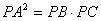 ,可得直径BC的长,要求 ,可得直径BC的长,要求 ,由△ACE∽△ADB得 ,由△ACE∽△ADB得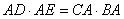 ,也就是求CA、BA的长。 ,也就是求CA、BA的长。

解:连结CE
∵PA是⊙O的切线,PBC是⊙O的割线
∴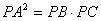
又PA=10,PB=5,∴PC=20,BC=15
∵PA切⊙O于A,∴∠PAB=∠ACP
又∠P为公共角,△PAB∽△PCA
∴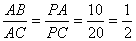
∵BC为⊙O的直径,∴∠CAB=900
∴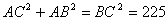
∴AC=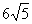 ,AB= ,AB=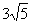
又∠ABC=∠E,∠CAE=∠EAB
∴△ACE∽△ADB,∴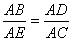
∴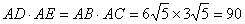 |

