|
方程与不等式的综合运用
班级 姓名 学号
学习目标:
1.进一步加强方程(组)与不等式(组)的之间的联系;
2.会运用方程(组)或不等式(组)模型解决实际问题, .在问题解决的过程中理解数学思想方法.
学习重点:方程(组)或不等式(组)的综合运用
学习难点:方程(组)或不等式(组)的综合运用
课前准备:
下列问题你能不能不用老师点拨就把别人讲懂?请先尝试看,看自己有无“漏洞”.
问题1:若不等式组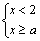 无解,那么 无解,那么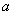 的取值范围是 的取值范围是
问题2:如果关于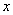 的方程 的方程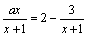 无解,则 无解,则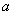 的值为 的值为
问题3:根据下列表格的对应值:
|
3.23 |
3.24 |
3.25 |
3.26 |
|
-0.06 |
-0.02 |
0.03 |
0.09 |
判断方程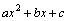 =0(a≠0,a,b,c为常数)一个解x的范围是( ) =0(a≠0,a,b,c为常数)一个解x的范围是( )
A、 3<x<3.23 B、 3.23<x<3.24 C、 3.24<x<3.25 D、 3.25<x<3.26
问题4:甲、乙两人完成一项工作,甲先做了3天,然后乙加入合作,完成剩下的工作,设工作总量为1,工作进度如下表:
则完成这项工作共需要的天数是 ( )
A.9 B.10 C.11 D.12
问题5:某商场计划拨款9万元从厂家购进50台电视机。已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元。
(1)商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案; (2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,你选择哪种进货方案?(3)若商场准备用9万元同时购进三种不同型号的电视机50台 |

