|
圆的有关概念
班级 姓名 学号
复习目标:
1、 知道圆、弧、弦、圆心角、圆周角等基本概念;认识圆的对称性;了解圆锥的侧面展开图是扇形。
2、 能用垂径定理,圆心角、弧、弦之间关系定理,圆周角定理及推论,等进行简单的运算和推理;会通过作图的方法理解确定圆的条件。
3、 会用折叠、旋转、圆的对称性及分类讨论的思想方法探索图形的有关性质,能将有关弦长、半径的实际计算问题转化成解直角三角形问题解决。
过程设计
一、知识回顾
 1、填空 1、填空
 基本概念: 弧、弦、圆心角、圆周角 基本概念: 弧、弦、圆心角、圆周角
 确定圆的条件: 确定圆的条件:
对称性:
垂径定理:
圆 基本性质: 圆心角、弧、弦的关系定理:
圆周角定理:同弧或等弧所对的圆心角是它所对的圆周角的
 推论:(1)同弧或等弧所的圆周角 推论:(1)同弧或等弧所的圆周角
(2)90°的圆周角所对弦是 ,
2、判断: (1)圆是轴对称图形,其对称轴是任意一条直径; ( )
(2)垂直于弦的直径平分弦,并且平分弦所对的弧; ( )
(3)过任意三点可确定一个圆; ( )
(4)任何三角形只有一个外接圆,一个圆也只有一个内接三角形;( )
(5)一条弦所对的圆心角是它所对的圆周角的2倍。 ( )
3.已知一定点P与⊙O上各点的距离最长为8cm,最短为2cm,则⊙O的直径为 .
4.△ABC内接于⊙O,AB=AC,∠A=50°,D是⊙O上一点,则∠ADB的度数为( )
(A)50° ; (B)65° ;(C)65°或50° ; (D)115°或65°
.5.下列命题中,正确的是( )
① 顶点在圆周上的角是圆周角; ② 圆周角的度数等于圆心角度数的一半;
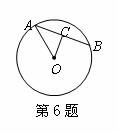 ③ ③ 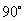 的圆周角所对的弦是直径; ④ 不在同一条直线上的三个点确定一个圆;⑤ 同弧所对的圆周角相等 的圆周角所对的弦是直径; ④ 不在同一条直线上的三个点确定一个圆;⑤ 同弧所对的圆周角相等
A.①②③ B.③④⑤ C.①②⑤ D.②④ |

