《现代教育报·新课程周刊》原创精品样稿
你追我赶话相遇
广州市越秀区教研员 周邦杰
要使物体相遇就必须同时满足位移关系和运动时间关系.
追及、相遇问题常常涉及到临界问题,分析临界状态,找出临界条件是解决这类问题的关键.速度相等是物体恰能追上或恰不相碰或间距最大或最小的临界条件.
一、避碰问题
避碰或追不上的条件是当两者同速时,两者位移差小于或等于初始时刻的距离时,两车不相撞或恰好不相撞.
例1 经检测汽车甲的制动性能:以标准速度20m/s在平直公路上行使时,制动后20s停下来.现甲在平直公路上以20m/s的速度行使,发现前方180m处有一货车乙以6m/s的速度同向匀速行使,司机立即制动,能否发生撞车事故?
解析:甲车加速度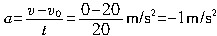 ,甲车减为与乙车同速的时间 ,甲车减为与乙车同速的时间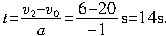 . .
在14s内甲车的位移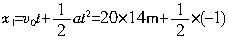 ×142m=182m. ×142m=182m.
乙车的位移x2=v2t=6×14m=84m.
两车位移差Δx=x1-x2=182m-84m=98m<180m.所以两车不相撞.
二、能否追上问题
对前面物体是匀减速运动时,要先判断追上前,前面物体是否早已静止,不要盲目列公式求解.
例2 甲、乙两车在同一条平直公路上运动,甲车以v1=10m/s的速度匀速行驶,经过车站A时关闭油门以a1=4m/s2的加速度匀减速前进;2s后乙车与甲车同方向以a2=1m/s2的加速度从同一车站A出发,由静止开始做匀加速直线运动,问乙车出发后多长时间追上甲车?
解析:甲、乙两车是同地点不同时开始运动,乙车出发时甲车具有的速度为v1t=v1-a1t=10m/s2×4m/s=2m/s,此时离甲车停止运动的时间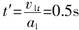 .甲车停止时已前进的位移 .甲车停止时已前进的位移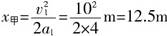 ,在0.5s内乙车前进的位移 ,在0.5s内乙车前进的位移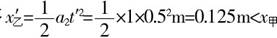 ,说明乙车在0.5s内追不上甲车,即乙车追上甲车时,甲车已经停止了运动.乙车追上甲,乙车应该从车站前进x甲,即 ,说明乙车在0.5s内追不上甲车,即乙车追上甲车时,甲车已经停止了运动.乙车追上甲,乙车应该从车站前进x甲,即 ,所以乙车出发后追上甲车的时间 ,所以乙车出发后追上甲车的时间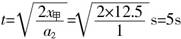 . .
三、间距极值问题
两物体同向运动,只要不都是匀速运动,当两物体的速度相等的时刻,两物体之间的距离有极值.如初速度为零的匀加速运动的物体追匀速运动物体,在速度相等时二者间距最大;匀减速运动的物体追匀速运动物体,在速度相等时二者间距最小.
(1) 在同一直线上的运动
例3 在京珠高速公路上的某段,有甲、乙两车同时同地同向出发,做直线运动,甲以初速度v甲=16m/s,加速度a甲=2m/s2做减速运动,乙以初速度v乙=4m/s,加速度a乙=1m/s2做匀加速运动.
求:(1)两车再次相遇前二者间的最大距离;
(2)两车再次相遇所需时间.
解析: 两车同时同地同向出发.因v甲>v乙,尽管甲做匀减速运动,乙做匀加速运动,在开始的一段时间内甲的速度大于乙的速度,两者间的距离越来越大,当甲减速,乙加速到二者速度相等时,二者间距离达到最大,此后,乙的速度大于甲的速度,二者间距离减小,当两者的位移相等时再次相遇.
两车间的距离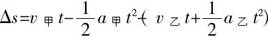
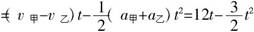
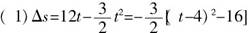 ,当t=4s时,有最大值,故最远距离 ,当t=4s时,有最大值,故最远距离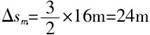
(2)当时Δs=0,两车再次相遇,即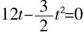
所以 t1=8s,t2=0(舍去)
(2) 不在一条直线的运动
例4 甲、乙两车分别沿互相垂直的公路行驶,甲车以8m/s的速度向北行驶,乙车以6m/s的速度向西行驶.一开始乙车在甲车的正东1km,从这点算起,经过多少时间两车的距离最短?这个距离又是多大?
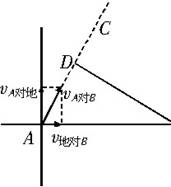
解析:以B(乙车)为参照物作出A(甲车)相对于B的速度,如图中沿直线AC方向.过B作AC的垂线,则BD的长度即为所求的最短距离,由于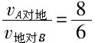 ,根据三角形的性质得BD=800m,AD=600m ,根据三角形的性质得BD=800m,AD=600m
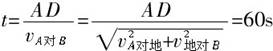 . .
|

