《现代教育报·新课程周刊》原创精品样稿
求解变力做功的常见方法
湖南 董马云
功是高中物理的重要概念,同学们对功的理解往往没有深入,用功能关系解题感到有点困难,尤其是对力做功的求解,特别是变力功的求解问题,同时这也是高考物理的重要考点,因为变力做功不能直接求解,需要通过一些特殊的方法,下面通过具体例题,介绍几种解决变力做功的常用方法。
一、动能定理法
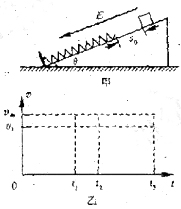
例1、(09年福建高考试卷)如图甲,在水平地面上固定一倾角为θ的光滑绝缘斜面,斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中。一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端,整根弹簧处于自然状态。一质量为m、带电量为q(q>0)的滑块从距离弹簧上端为s0处静止释放,滑块在运动过程中电量保持不变,设滑块与弹簧接触过程没有机械能损失,弹簧始终处在弹性限度内,重力加速度大小为g。
 (1)求滑块从静止释放到与弹簧上端接触瞬间所经历的时间t1 (1)求滑块从静止释放到与弹簧上端接触瞬间所经历的时间t1
(2)若滑块在沿斜面向下运动的整个过程中最大速度大小为vm,求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W;
(3)从滑块静止释放瞬间开始计时,请在乙图中画出滑块在沿斜面向下运动的整个过程中速度与时间关系v-t图象。图中横坐标轴上的t1、t2及t3分别表示滑块第一次与弹簧上端接触、第一次速度达到最大值及第一次速度减为零的时刻,纵坐标轴上的v1为滑块在t1时刻的速度大小,vm是题中所指的物理量。(本小题不要求写出计算过程)
解析:本题考查的是电场中斜面上的弹簧类问题。涉及到匀变速直线运动、运用动能定理处理变力功问题、最大速度问题和运动过程分析。
(1)滑块从静止释放到与弹簧刚接触的过程中作初速度为零的匀加速直线运动,设加速度大小为a,则有
qE+mgsin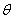 =ma ① =ma ①
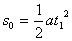 ② ②
联立①②可得
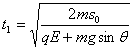 ③ ③
(2)滑块速度最大时受力平衡,设此时弹簧压缩量为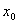 ,则有 ,则有
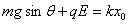 ④ ④
从静止释放到速度达到最大的过程中,由动能定理得
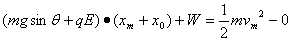 ⑤ ⑤
联立④⑤可得
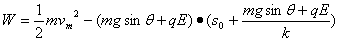 s s
(3)如图
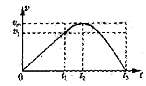
点评:利用动能定理可以求变力做功,并且用动能定理只要求始末状态,不要求中间过程。这是动能定理比牛顿运动定律优越的一个方面。
二、 能量守恒法
例2. 如图所示,质量m为2kg的物体,从光滑斜面的顶端A点以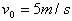 的初速度滑下,在D点与弹簧接触并将弹簧压缩到B点时的速度为零,已知从A到B的竖直高度 的初速度滑下,在D点与弹簧接触并将弹簧压缩到B点时的速度为零,已知从A到B的竖直高度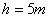 ,求弹簧的弹力对物体所做的功。 ,求弹簧的弹力对物体所做的功。
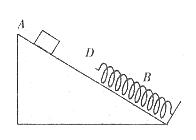
解析:由于斜面光滑,故机械能守恒,但弹簧的弹力是变力,弹力对物体做负功,弹簧的弹性势能增加,且弹力做功的数值与弹性势能的增加量相等。取B所在水平面为零参考面,弹簧原长处D点为弹性势能的零参考点,则
对状态A: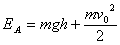
对状态B:
由机械能守恒定律得:
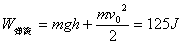
点评:如果物体只受重力和弹力作用,或只有重力或弹力做功时,满足机械能守恒定律。如果求弹力这个变力做的功,一般我们都可以用机械能守恒定律求功。
三、用数列求和公式求变力的功
例3、线段AB长S分成n等份,一质量为m的质点由A从静止出发,以加速度a向B运动,当质点每达一等份点时,所受外力适时调整,使加速度增加a/n,如此反复,求质点到达B点时,外力所做总功为多少?
解析:质点运动过程中,外力F不断调整,本题属于变力做功,但在每一分位移段内,外力F为恒力,故可以先将外力F在每段做功的通项表达式求出,再用求和法得出总功,令物体经第1、第2、第3、……第n段位移时所受外力分别为F1、F2、……Fn则有:
W1=F1S1=ma.· , W2=F2S2=m(a+ , W2=F2S2=m(a+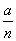 )· )· , W3=F3S3=m(a+2 , W3=F3S3=m(a+2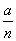 )· )· , ,
------- Wn=FnSn=m[a+(n-1)2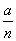 ]· ]· , ,
故W总=W1+W2+W3+W4+----+Wn=m· [na+ [na+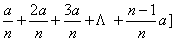 = =
点评:如果物体所受作用力或速度的变化具有某些特殊规律,可依据基本物理定理求出力或功的通项表达式,再利用数列求和法巧妙计算出结果。
四 用公式W=Pt求解
例4 (09年上海物理)质量为5´103 kg的汽车在t=0时刻速度v0=10m/s,随后以P=6´104 W的额定功率沿平直公路继续前进,经72s达到最大速度,设汽车受恒定阻力,其大小为2.5´103N。求:(1)汽车的最大速度vm;(2)汽车在72s内经过的路程s。
解析:当机车的功率恒定后,当机车继续加速过程中,牵引力不断减小,当速度达到最大值时,机车所受牵引力达到最小值,与阻力相等.在这段时间内机车所受阻力可认为是恒力,牵引力是变力,因此,机车做功不能直接用W=Fscosa来求解,但可用公式W=Pt来计算.
(1)当达到最大速度时,P==Fv=fvm,vm==m/s=24m/s
(2)从开始到72s时刻依据动能定理得:
Pt-fs=mvm2-mv02,解得:s==1252m。
点评:对于交通工具以恒定功率运动时,都可以根据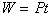 来求牵引力这个变力所做的功。 来求牵引力这个变力所做的功。
五 平均力法
例5. 用铁锤将一铁钉击入木块,设木块对铁钉的阻力与铁钉钉入木块内的深度成正比。在铁锤击第一次时,能把铁钉击入木块内1cm,问击第二次时,能击入多深?(设铁锤每次做功都相等)
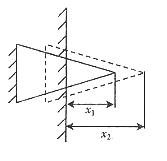 解析:铁锤每次做功都是克服铁钉阻力做功,但摩擦阻力不是恒力,其大小与深度成正比。 解析:铁锤每次做功都是克服铁钉阻力做功,但摩擦阻力不是恒力,其大小与深度成正比。 ,可用平均阻力来代替。 ,可用平均阻力来代替。
如图所示,第一次击入深度为 ,平均阻力为 ,平均阻力为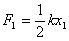 ,做功为: ,做功为:
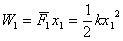
第二次击入深度为 到 到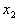 ,平均阻力为: ,平均阻力为:
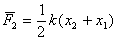
位移为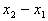 做功为: 做功为:
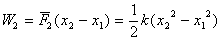
两次做功相等: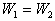
解后有: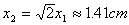
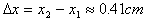
点评:如果力的方向不变,力的大小对位移按线性规律变化时,可用力的算术平均值(恒力)代替变力,利用功的定义式求功。类似的例子还有很多,像求弹簧弹力做功时,也可以用这种办法。
六 图象法
例6. 放在地面上的木块与一劲度系数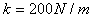 的轻弹簧相连。现用手水平拉弹簧,拉力的作用点移动 的轻弹簧相连。现用手水平拉弹簧,拉力的作用点移动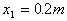 时,木块开始运动,继续拉弹簧,木块缓慢移动了 时,木块开始运动,继续拉弹簧,木块缓慢移动了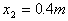 的位移,求上述过程中拉力所做的功。 的位移,求上述过程中拉力所做的功。
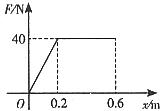 解析:由题意作出 解析:由题意作出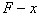 图象如图所示,在木块运动之前,弹簧弹力随弹簧伸长量的变化是线性关系,木块缓慢移动时弹簧弹力不变,图线与横轴所围梯形面积即为拉力所做的功。即 图象如图所示,在木块运动之前,弹簧弹力随弹簧伸长量的变化是线性关系,木块缓慢移动时弹簧弹力不变,图线与横轴所围梯形面积即为拉力所做的功。即
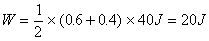
点评:一个看似复杂的变力做功问题,用常规方法无从下手,但通过图象变换,就使得解题过程简单、明了。可见,图象法是一个很好的解题方法,值得掌握。
|

