向心力齐动员
一、转盘模型
物体做圆周运动时都会受到向心力的作用,其所受的向心力都是由合外力提供,因此各种圆周运动中物体的受力分析,成为解决圆周运动的重要过程,善于抓住某些典型的圆周运动模型,就容易做到事半功倍、轻松快捷解决问题.
例1 如图5所示,在绕竖直轴匀速转动的水平圆盘盘面上,离轴心r=20cm处放置一小物块,其质量为m=2kg,A与盘面间相互作用的最大静摩擦力为其重力的k=0.5倍,试求:
例2 
(1)当圆盘转动的角速度?棕=2rad/s时,物块与圆盘间的摩擦力大小多大?方向如何?
(2)欲使A与盘面间不发生相对滑动,则圆盘转动的最大角速度多大?(g取10m/s2)
解析:(1)物块竖直方向受重力mg、支持力FN,水平方向受静摩擦力f,静摩擦力提供物块随圆盘转动的向心力,即有:f=m?棕2r=2×22×0.2N=1.6N,方向为指向圆心.
(2)要使物块不相对圆盘滑动,应使物块转动的向心力小于或等于物块所受的最大静摩擦力,即:
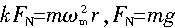
代入数据解得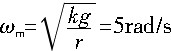
点评:物体做圆周运动,必有向心力,要对做圆周运动的物体进行受力分析,一定要注意向心力是效果力,可以由一个力提供,也可以由一个力的分力提供,还可由多个力的合力来提供.
二、轻绳模型
例2 如图6所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学用绳拴着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,问:
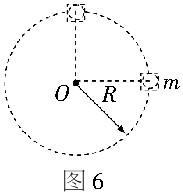
(1) 要使盒子在最高点时盒子与小球之间恰好无作用力,则该盒子做匀速圆周运动的周期为多少?
(2) 若盒子以第(1)问中周期的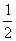 做匀速圆周运动,则当盒子运动到图6所示球心与O点位于同一水平面位置时,小球对盒子的哪些面有作用力,作用力为多大? 做匀速圆周运动,则当盒子运动到图6所示球心与O点位于同一水平面位置时,小球对盒子的哪些面有作用力,作用力为多大?
解析: (1)设此时盒子的运动周期为T0,因为在最高点时盒子与小球之间刚好无作用力,因此小球仅受重力作用.根据牛顿运动定律得:
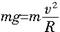 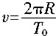 解之得: 解之得: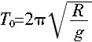
(2)设此时盒子的运动周期为T,则此时小球的向心加速度为: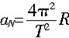 由第一问知: 由第一问知: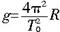 且 且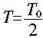
由上述三式知:aN=4g
设小球受盒子右侧面的作用力为F,受上侧面的作用力为N,根据牛顿运动定律知:在水平方向上:F=maN即:F=4mg;在竖直方向上:N+mg=0,即:N=-mg
因为F为正值、N为负值,所以小球对盒子的右侧面和下侧面有作用力,分别为4mg和mg.
点评:虽然绳子的拉力作用在盒子上,但应选择其中的小球作为研究对象进行受力分析.
三、轻杆模型
例3 如图7所示,长L=0.5m,质量可以忽略的细杆,其下端固定于O点,上端连接着一个质量m=2kg的小球A,A绕O点做圆周运动,在A通过最高点时,试讨论在下列两种情况下杆的受力(g取10m/s2):
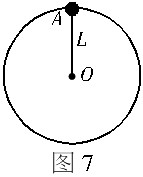
(1)当A的速率v1=1m/s时;(2)当A的速率v2=4m/s时.
解析:小球在最高点处所受向心力由杆的弹力和小球重力的合力提供,若小球的线速度大于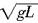 = =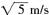 时,杆受到拉力;小于 时,杆受到拉力;小于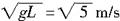
时,杆受压力.
(1)当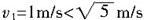
时,小球受向下的重力mg和向上的支持力N
由牛顿第二定律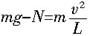
,得
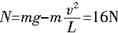
,即杆受小球的压力16N.
(2)当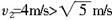
时,小球受向下的重力mg和向下的拉力F;
由牛顿第二定律 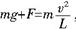
,得
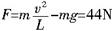 ,即杆受小球的拉力44N. ,即杆受小球的拉力44N.
点评:轻杆模型属于有支撑的圆周运动.在竖直面内运动时,最高点速度最小为零,杆上的力可以是拉力,也可以是支持力.
四、圆锥摆模型
例4 如图8甲所示,一根细线上端固定在S点,下端连一小铁球A,让小铁球在水平面内做匀速圆周运动,此装置构成一个圆锥摆(不计空气阻力),下列说法正确的是( )
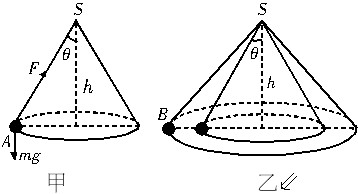
图 8
A. 小球做匀速圆周运动时,受到重力、绳子拉力和向心力作用
B. 小球做匀速圆周运动时的角速度一定大于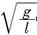 (l为摆长) (l为摆长)
C. 另有一个圆锥摆B,摆长更大一点,两者悬点相同,如图8乙所示.如果改变两小球的角速度,使两者恰好在同一水平面内做匀速圆周运动,则B球的角速度大于A球的角速度
D. 如果两个小球的质量相等,则在图乙中两条细线的拉力相等
解析:向心力是效果力,分析圆周运动的物体受力时不能加上向心力,故A项错误;小球运动过程中受到拉力和重力作用,二者的合力提供向心力,即有:
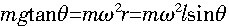
所以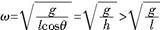
即选项B正确,选项C错误;
又由图可知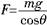 ,故选项D错误.正确答案为B. ,故选项D错误.正确答案为B.
点评:圆锥摆问题实质上是物体在水平面内的圆周运动,只是其向心力由绳子的拉力和重力共同提供.处理时要充分利用锥摆与竖直方向的夹角和重力已知来求向心力问题. |

